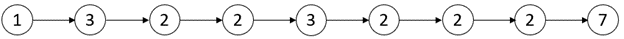A critical point in a linked list is defined as either a local maxima or a local minima.
A node is a local maxima if the current node has a value strictly greater than the previous node and the next node.
A node is a local minima if the current node has a value strictly smaller than the previous node and the next node.
Note that a node can only be a local maxima/minima if there exists both a previous node and a next node.
Given a linked list head, return an array of length 2 containing[minDistance, maxDistance]whereminDistanceis the minimum distance between any two distinct critical points andmaxDistanceis the maximum distance between any two distinct critical points. If there are fewer than two critical points, return[-1, -1].
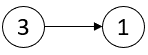
Input: head = [3,1] Output: [-1,-1] Explanation: There are no critical points in [3,1].
Input: head = [5,3,1,2,5,1,2] Output: [1,3] Explanation: There are three critical points: - [5,3,1,2,5,1,2]: The third node is a local minima because 1 is less than 3 and 2. - [5,3,1,2,5,1,2]: The fifth node is a local maxima because 5 is greater than 2 and 1. - [5,3,1,2,5,1,2]: The sixth node is a local minima because 1 is less than 5 and 2. The minimum distance is between the fifth and the sixth node. minDistance = 6 - 5 = 1. The maximum distance is between the third and the sixth node. maxDistance = 6 - 3 = 3.
Input: head = [1,3,2,2,3,2,2,2,7] Output: [3,3] Explanation: There are two critical points: - [1,3,2,2,3,2,2,2,7]: The second node is a local maxima because 3 is greater than 1 and 2. - [1,3,2,2,3,2,2,2,7]: The fifth node is a local maxima because 3 is greater than 2 and 2. Both the minimum and maximum distances are between the second and the fifth node. Thus, minDistance and maxDistance is 5 - 2 = 3. Note that the last node is not considered a local maxima because it does not have a next node.
- The number of nodes in the list is in the range
[2, 105]. 1 <= Node.val <= 105
# Definition for singly-linked list.# class ListNode:# def __init__(self, val=0, next=None):# self.val = val# self.next = nextclassSolution: defnodesBetweenCriticalPoints(self, head: Optional[ListNode]) ->List[int]: prev=headcurr=head.nextfirstlocal=-1prevlocal=-1i=0ret= [-1, -1] whilecurr.next: if (prev.val<curr.valandcurr.val>curr.next.val) \ or (prev.val>curr.valandcurr.val<curr.next.val): iffirstlocal==-1: firstlocal=ielifret[0] ==-1: ret= [i-prevlocal, i-firstlocal] else: ret= [min(ret[0], i-prevlocal), i-firstlocal] prevlocal=iprev=currcurr=curr.nexti+=1returnret